Los modelos matemáticos y los mapas de la modernidad

Comienzo este post con dos ideas, que me han surgido a colación de una conversación que mantuvimos el otro día en clase. La primera tiene que ver con el hecho de que, para aquellos sistemas formales en los que el correlato con la realidad no es evidente, comentábamos que precisaban de un modelo que les sirviera de referente, en base al cual podían construir una imagen de dicho sistema, y le sirviera a la vez de criterio para establecer el valor de verdad de sus teoremas. Este modelo no es en absoluto algo evidente, sino que muy bien puede poseer un carácter abstracto que dificulte su representación, pues no necesariamente ha de adecuarse a nuestro modo natural de entender el mundo. En sentido amplio, el modelo podría entenderse como una representación construida a partir del sistema formal, y que a la vez sirve de marco de referencia. La segunda idea tiene que ver con el hecho de que los físicos son conscientes de que en la matemática hay muchos modelos, hay muchos mundos posibles, y no todos necesariamente nos pueden decir algo del mundo de la naturaleza, del mundo en el que vivimos y en el que nos movemos, que es el que ellos estudian. Ya de Broglie ponía de manifiesto cómo, desde la perspectiva matemática, los sistemas axiomáticos son simplemente sistemas cuyo valor estriba en la coherencia interna, cuando lo que busca el físico es si esos sistemas reflejen la realidad de las cosas. «Entre las teorías lógicamente posibles, las hay, sin embargo, que están más cerca de la realidad física, mejor adaptadas en todo caso a la intuición del físico y más aptas a secundar sus esfuerzos». Ello nos lleva a un segundo problema, como es el de la posibilidad de que ‘este modelo’ en concreto sirva para describir la realidad o no.

El reto es ciertamente complejo. Porque ese modelo matemático no se crea de buenas a primeras, sino que se va creando conforme el propio sistema formal se va desarrollando, y ya digo, por lo general con un carácter bastante abstracto. El modelo es como una foto: mediante el juego de los axiomas, las reglas de transformación, etc., se van obteniendo los distintos teoremas y, en consideración con todo ello se va elaborando el modelo. Para que el modelo sea adecuado, su construcción debe ser coherente; y así, una vez ha sido creado, sirve para contrastar las verdades de los sucesivos teoremas que se vayan demostrando. Y hay que ver si ese modelo construido únicamente a base de condicionantes internos (del propio ejercicio matemático) puede decirnos algo válido de la realidad natural, y en qué medida lo puede hacer. ¿Es verdadero? ¿Representa de alguna manera, aunque sea imperfectamente, la realidad de las cosas?

Si lo pensamos, parece que esto sea un contrasentido: elaboramos un sistema axiomático el cual nos da lugar a un modelo, el cual nos sirve posteriormente para calificar la verdad o falsedad de los sucesivos teoremas; estando por ver, además, que dicho modelo se adecúa o no a la realidad física. Pero es así. Estos modelos bien pueden llevarnos a realidades imaginarias, bien pueden llevarnos a nuevas representaciones de lo real ajenas a nuestra experiencia actual, ayudándonos a comprenderla mejor (caso paradigmático es el de la geometría de Riemann y la curvatura del espacio-tiempo según la teoría de la relatividad de Einstein).

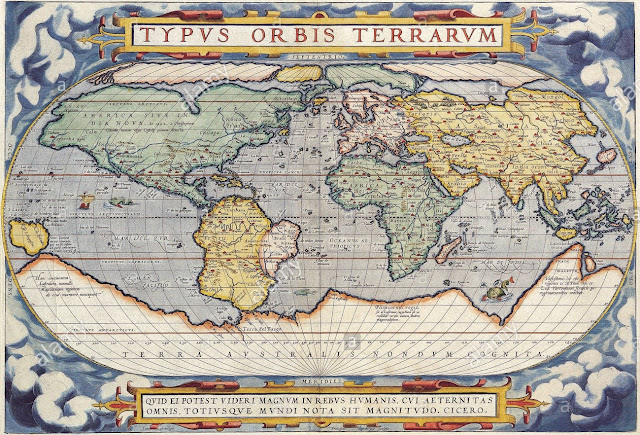
Ya digo, comentando esto el otro día en clase se me ocurrió una analogía que puede ser útil para clarificarlo. Pensemos en un mapa geográfico; pero un mapa no de los actuales, sino de los de hace algunos siglos, cuando se comenzaron a surcar los mares. Si ahora observamos un mapa actual, seguramente obtenido mediante satélites, etc., veremos que son de una exactitud asombros; muy distinto es observar un mapa de los que elaboraron en su día los primeros navegantes. De hecho, cuando ahora vemos esos mapas, los vemos deformados. La diferencia está en que los mapas actuales son tan exactos porque se han podido elaborar ‘desde fuera’, desde un punto de observación distante, lo que permite una perspectiva óptima; pero estos navegantes aventureros sólo podían hacer sus mapas ‘desde dentro’, desde los mismos mares, costas y tierras que estaban tratando de representar.

Imaginemos que somos uno de esos primeros geógrafos, el famoso Abraham Ortelius, por ejemplo; y que, después de un período de intenso trabajo, elaboramos un mapa, mediante el cual representamos una zona geográfica del globo, según nuestras posibilidades. No necesariamente coincide con la realidad (de hecho, no coincide) pero a nosotros nos sirve. Incluso, una vez dibujado, muy bien lo podemos utilizar para medir distancias, ubicar pueblos y ciudades, etc. Tomándolo como referencia, podemos saber si es cierto que dos ciudades están cercanas, o si este golfo tiene esta extensión o no, etc. Pues bien, este mapa puede considerarse un modelo de la realidad. Seguramente otro geógrafo elaboraría un mapa diferente, obteniendo un modelo distinto. Pero todos estos mapas serían modelos de la realidad, representaciones suyas, independientemente de que algunos fueran más adecuados que otros, o que incluso no tuvieran nada que ver con ella. En todos los casos, haría falta contrastarlo con la realidad de las cosas (que es lo que hizo Einstein con la geometría de Riemann). De alguna manera el modelo se construye ‘desde dentro’, desde el trabajo del geógrafo o del matemático, con la idea en principio de que pueda ser de utilidad para comprender la realidad de las cosas, para lo cual hará falta calificarlo ‘desde afuera’.

Creo que esta idea nos puede servir para comprender mejor lo que es el modelo para las matemáticas. La utilidad que tiene el modelo es importante, como la tiene un mapa. Si queremos saber la distancia de una ciudad a otra, no hemos de medirla in situ sino que podemos medirla sobre el mapa, algo que desde luego es mucho más sencillo. Con el modelo matemático ocurre algo igual: una vez ha sido elaborado y contrastado, sirve de un modo más sencillo para calificar los teoremas y las proposiciones. En un sistema formal, todo modelo tiene que ver de algún modo con la interpretación del sistema; se va confeccionando a la luz de los axiomas, reglas, etc., y a la vez estos deben ser consistentes con tal interpretación. Una vez hecho esto, hay que seguir comprobando que todos los teoremas que surjan según las reglas de transformación, que las proposiciones resultantes continúen siendo verdaderas, para lo cual nos sirve dicho modelo: si el modelo es verdadero, y el teorema ‘encaja’ en él, será verdadero también. De este modo se puede afirmar, con Raguní, que «la regla [las reglas de transformación] cuando actúa sobre axiomas interpretados en el modelo, produce teoremas verdaderos en el modelo, sobre los cuales puede todavía actuar produciendo otros teoremas verdaderos. Y así sucesivamente producirá sólo teoremas verdaderos para el modelo». Así, cada vez más enunciados formales del sistema irán resultando proposiciones verdaderas, consolidando así dicho modelo.

Pero también tiene otra utilidad muy importante, como es la de ahorrarnos mucho trabajo a la hora de establecer o de aplicar la verdad de un teorema en un sistema de cálculo formal, el cual puede ser visto a la luz de distintos modelos; así, «cualquier teorema, aunque sea formidablemente largo y difícil (tal vez descubierto también gracias a la ayuda ‘visual’ de un modelo concreto), vale automáticamente (esto es, sin necesidad de repetir la demostración) para todos los modelos correctos con respecto a las reglas de deducción del sistema».

Esto es especialmente interesante, por dos motivos. Primero porque, para la confección de dicho sistema formal, no viene mal ‘echar mano’ de la experiencia que podamos tener con el entorno o con otros modelos, y que nos sirva para desarrollar ciertos teoremas a los cuales quizás no hubiéramos llegado de no contar con esa experiencia (procedimiento que, como se puede suponer, no es exclusivo, y muy bien los teoremas pueden derivarse según el desarrollo meramente formal, que es de hecho como suele ocurrir). Y el segundo porque, si nos fijamos, no tiene sentido hablar de verdad en el seno de un sistema formal. ¿De qué verdad estamos hablando? En principio, toda verdad lógica es una verdad inherente a un sistema, y sólo concierne a la coherencia interna del mismo. Pero ¿nos referimos a esto cuando hablamos de verdad?, ¿no pensamos en el correlato con la realidad de un pensamiento, o de un juicio? En este sentido y en este contexto, sólo cabría hablar de verdad según la interpretación que se dé a los símbolos y a las reglas del sistema formal; es decir, sólo cabe hablar de verdad cuando los referimos a los modelos, de modo que se puede afirmar que «la utilidad indiscutible del lenguaje matemático se pone de manifiesto sólo cuando éste viene interpretado por los modelos correctos, concretándose así en proposiciones significativas». Ya digo, otra cosa es que dicho modelo tenga que ver algo con la realidad. Nosotros podemos confeccionar un sistema axiomático, coherente en sí mismo, pero que, en definitiva, poco nos diga de la realidad. De eso ya se ocuparán los físicos.

Resuenan aquí las palabras de Russell, cuando dijo que los matemáticos no son sino un conjunto de personas hablando no se sabe de qué, ni sabiendo si lo que dicen es verdadero o no. Lo que hace un sistema formal no es sino establecer un lenguaje depurado de cualquier significado semántico, para quedarse en el mero valor simbólico que el propio creador le haya querido dar, separándolo de cualquier lenguaje al uso. Tendremos así, un sistema formal, coherente en sí mismo, que es susceptible de ser verificado por su consistencia ante modelos… verdaderos. A veces dirigirán el concierto los modelos verdaderos, a veces dirigirá el concierto el sistema formal, ofreciéndonos nuevos modos de comprender lo real.