La relación entre el trabajo y el calor de un sistema

Vimos en este post cómo Joule fue capaz de poner en común dos fenómenos en principio dispares: un trabajo mecánico con la generación de calor. Y vimos cómo, una vez salvada la sorpresa inicial, la cosa no era tan descabellada pues, en el fondo se trataban de dos formas de energía. Inicialmente, Joule fue capaz de establecer una proporcionalidad entre el trabajo realizado y el calor generado. El siguiente paso fue averiguar cómo poner en común el trabajo o energía mecánica con el calor o energía calorífica, desde una base experimental y científica.

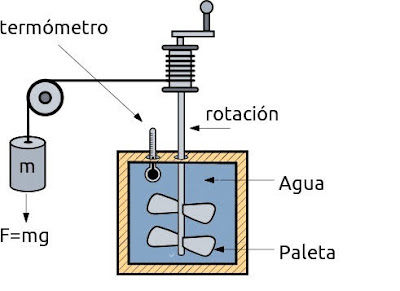
Empecemos por lo más fácil, que es calcular la energía partiendo del trabajo generado por las pesas. ¿Cuál fue la cantidad de trabajo que desapareció en el experimento de Joule? Si soltamos unas pesas, lo normal es que caigan con rapidez, con un movimiento uniformemente acelerado, hasta que den con el suelo. Pero, si nos fijamos, en el esquema de Joule no es así, sino que, al estar enganchadas a las paletas (a las que mueven) que giran en el interior del tanque, el agua genera una resistencia a las paletas y estas a la caída libre de las pesas, por lo que no caen en caída libre, sino lentamente. Es la propia resistencia del agua al giro de las paletas lo que evita que las pesas caigan en caída libre. Quedémonos con este dato, porque es importante: que, a pesar de estar las pesas sometidas a la gravedad, no se aceleran uniformemente como correspondería a una caída libre, sino que esa aceleración que debían tener se ve frenada por la resistencia que el agua ofrece a las palas.

Supongamos que hemos diseñado el mecanismo para que las pesas desciendan a velocidad constante, es decir, que su aceleración se vea anulada gracias a la resistencia del agua al giro de las paletas, algo que se puede conseguir fácilmente después de algunos tanteos. No olvidemos que estamos trabajando con un sistema conservativo, es decir, que mantiene constante su energía total la cual, en el caso de móviles (como las pesas) consta de una parte de energía potencial y otra parte de energía cinética. Si tomamos dos puntos de su trayectoria, A y B, en A tendrán una E_pA y una E_cA, y en B una E_pB que será menor que en A y una E_cB que, en el fondo, es la misma energía cinética que en A, pues hemos diseñado el experimento para que la velocidad sea la misma. En principio, la disminución de energía potencial debía ser la misma que el aumento de energía cinética, que es lo que ocurre, por ejemplo, en una caída libre; como no es el caso, ya que hemos diseñado el experimento para que la caída libre se vea frenada por la resistencia que ofrece el agua a las palas, este aumento de energía cinética que ha dejado de darse es, en el fondo, esa variación de energía que se sitúa en el origen de ese trabajo ‘que desaparece’. La energía potencial de las pesas ha disminuido sin incrementarse su energía cinética, y es esta falta de incremento de la energía cinética la que nos dice qué energía ‘ha desaparecido’, que será la que se haya transmitido, mediante las palas, al agua. Ese trabajo que desaparece de las pesas es el que provoca la agitación del agua y el cambio de su estado, elevándose su temperatura por rozamiento, calentándose. De este modo, ese cambio de estado del agua se interpreta como un cambio de energía (calorífica), el cual se mide por medio de la cantidad de trabajo que desapareció del ambiente (de las pesas).

Si E₁ y E₂ son los estados energéticos inicial y final del sistema en dos momentos concretos, tenemos que:

E₂ - E₁ = -W

W es el trabajo que ha desaparecido, es decir, la energía cinética que no se ha generado y que, a la postre, viene a ser la misma que lo que ha disminuido la potencial. Así, la diferencia de energía entre el estado final y el inicial es igual al trabajo que desaparece; de ahí el signo negativo de W: el signo menos de -W se debe a que es trabajo que realiza el sistema; si el sistema recibiera trabajo tomaría el valor positivo, y el sistema se enfriaría, no se calentaría. Se suele adoptar el criterio de que, si el trabajo es realizado por el sistema, su signo es negativo, y si es recibido por el sistema, positivo.

Decíamos que el trabajo era igual al cambio de energía potencial, dado que la energía cinética es la misma en ambos puntos. Si las pesas pesan P, nos queda que W = P·h₂ – P·h₁ = P · (h₂ – h₁). En el experimento de Joule, h₂ es más pequeño que h₁, es decir, en el instante 2 las pesas están más abajo que en el 1, por lo que la diferencia es negativa. Este valor negativo, multiplicado por el negativo de W nos da un valor positivo, que se corresponde con el incremento de energía que se obtiene en el depósito de agua (el agua se calienta, E₂ > E₁).

Como el trabajo que desaparece se puede medir perfectamente, sabemos cuál es la variación energética que experimenta el sistema, sabemos cuánto calor se ha generado en el agua. Hay una conexión entre trabajo realizado y calor generado. Esto es algo que ocurre siempre, es decir, si se tiene un sistema termodinámico, todo par de estados a diferentes temperaturas se pueden conectar mediante la realización de un trabajo adiabático: partiendo de uno de ellos, y realizando el trabajo correspondiente, siempre se puede llegar al otro. Que hasta la fecha haya ocurrido siempre, nos permite extrapolar razonablemente que es algo que ocurrirá siempre. Podemos pasar de un estado de un sistema a otro, siempre, realizando el trabajo oportuno.