El fundamento geométrico de la materia en Platón

Pudiera pensarse que hoy en día, el planteamiento que poseía Platón sobre la estructura de la materia es algo totalmente anacrónico y superado; seguramente sea así, aunque no es menos cierto que se pueden encontrar en él algunas intuiciones relevantes. Algo tendrá que ver sin duda los orígenes de los que parte su pensamiento, que no es otro que el de los filósofos que le precedieron, y que pueden agruparse en dos corrientes: los materialistas, para quienes el fundamento de la materia era a su vez algo material (el agua, los cuatro elementos, etc.), y los idealistas, que postulaban dicho fundamento en algo ideal, a saber: los números.

Platón fue un pensador que viajó mucho y que vivió mucho (como se suele decir), aprendiendo de primera mano doctrinas de ambas tradiciones. Seguramente se pueda decir que se sintió especialmente atraído por el pensamiento pitagórico y su planteamiento del fundamento numérico del universo; algo que influyó no sólo en su cosmología, sino también en su teoría de la materia. A la estela de esta tradición, lo que hizo fue buscar el fundamento de la materia, el arjé, en lo matemático. Si lo pensamos, es algo que no deja de llamar la atención: ¿cómo lo matemático, lo geométrico, puede ser el fundamento de la materia, aquella fuente originaria de la que brotan todas las cosas materiales? La verdad es que su postura, ya digo, un tanto anacrónica, es cuanto menos sorprendente y creativa; y, lo que a mi modo de ver es más importante, tuvo dos consecuencias muy importantes: a) la de ‘leer’ la realidad en términos matemáticos, postura que será continuada por científicos medievales hasta llegar a la modernidad, momento en el que se origina la conocida como nuova scienza, en la que dicha metodología se consolida, danto tantos y tan buenos frutos; b) la limitación de este enfoque a la hora de estudiar lo que sea la materia en sí misma, mostrando las dificultades de poder explicar la materia metafísicamente en términos matemáticos.

En su teoría de la materia, Platón parte de la idea de que ésta estaba compuesta por los cuatro elementos fundamentales: tierra, agua, aire y fuego, a los cuales subyacía un sustrato común, un principio universal, pero que no era material sino de carácter geométrico: el triángulo. Decisión que no fue arbitraria ni ingenua: hoy en día el método de la triangulación es ampliamente utilizado en topografía, por ejemplo. ¿Qué tiene de particular el triángulo? Pues que, a base de triángulos, se podía cubrir cualquier superficie.

Su razonamiento venía a ser como sigue. Platón partió del hecho de que todos los cuerpos poseían volumen, el cual era definido por una superficie, por su superficie; a su vez, toda superficie puede ser extendida sobre un plano (como en nuestros mapamundis o atlas geográficos) y, consecuentemente, puede ser dividida en triángulos, de cualquier tipo que sean. Y no importa el tipo de triángulos en que se divida, pues todo triángulo puede ser a la vez subdividido a la larga en dos tipos de triángulos: el rectángulo escaleno y el isósceles. Pues bien, estos dos tipos de triángulos son los que constituyen el principio último de la realidad, triángulos elementales que emplearía el Demiurgo para dar la existencia a las cosas partiendo del modelo de los triángulos ideales, tal y como explica Platón en el Timeo. Como dice Melogno, «podemos establecer que la estructura última está compuesta por estos dos triángulos ―rectángulo escaleno e isósceles― desde el momento en que una vez que dividiendo cualquier superficie obtenemos alguno de los dos, y podemos seguir efectuando divisiones que reproduzcan de modo invariante el triángulo obtenido, por lo que éste tendría el carácter irreductible que le fue negado respectivamente a los elementos, al volumen y a la superficie».

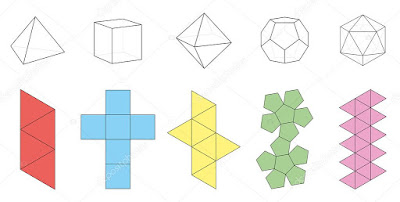
Pero claro, el caso es que los triángulos son bidimensionales, y los cuerpos tridimensionales. ¿Cómo pasar de una unidad originaria plana, a los cuerpos reales con volumen? En el planteamiento platónico, esto correspondía a cierto tipo de entidades, también estructurales pero híbridas, en el sentido de que poseían volumen, pero formadas de modo estrictamente puro por estos tipos de triángulos. ¿Qué entidades son estas? Pues los poliedros regulares: tetraedro, hexaedro, octaedro, dodecaedro e icosaedro, cuyas caras son todas polígonos regulares, y que podían a su vez dividirse en triángulos fundamentales. Cada uno de estos poliedros tenía volumen, y su superficie podía ser desplegada en un plano, y dividida en triángulos elementales. Y con los poliedros regulares ya se podría apreciar el volumen que en los triángulos elementales estaba ausente. De alguna manera, los triángulos son una especie de ‘átomos planos’, unos átomos geométricos a partir de los cuales, mediante procesos de orden y simetría, como dice Wilczek, se obtienen construcciones cada vez más ricas y complejas, formando la materia tal y como la conocemos.