El 'caso Kepler'

A raíz del anterior post, un amigo me comentó por qué no hablaba un poco más detenidamente del ‘caso Kepler’, pues ya me había leído alguna otra referencia al respecto, y tenía curiosidad. Así que nada, a ello voy, en la medida de mis posibilidades. Sabido es que Kepler era afín a la teoría heliocéntrica de Nicolás Copérnico (1473-1543); teoría que —como es sabido— ya fue propuesta mucho tiempo antes (en el siglo III a. de C.) por Aristarco de Samos, aunque no tuvo muchos seguidores. Pues bien, mucho tiempo después, Nicolás Copérnico fue el científico que recuperó dicha teoría y la estableció como el modelo más plausible para describir el cosmos conocido. Y en este contexto, viene al escenario nuestro querido Johannes Kepler (1571-1630).

Su punto de partida fue, pues, la herencia que legó Copérnico: los planetas se movían según órbitas circulares alrededor del sol. Y su primera intención fue la de demostrar la hipótesis copernicana. En esto no se diferenciaba de buena parte de los astrónomos de la época. Su novedad —y su grandeza— fue otra distinta. Lo llamativo del caso Kepler ―a mi modo de ver― no fue tanto la demostración y descripción más afinada de las órbitas celestes ―que también― como el cambio de paradigma que supuso su aportación, y que daría origen a lo que poco más tarde con Newton y Galileo se consolidaría como ‘ciencia moderna’.

Los argumentos que se solían esgrimir en la época (así el mismo Copérnico) para fundamentar el heliocentrismo no eran estrictamente físicos o científicos (tal y como hoy entendemos la física o la ciencia), sino metafísicos. Y Kepler no era ajeno a este planteamiento, pues de alguna manera entendía que el orden cósmico no era sino un fiel reflejo de la perfección del pensamiento divino. Su gran novedad fue que él no se quedó en este enfoque, fruto del cual lo que primaba era sobre todo la descripción geométrica del sistema solar, sino que comenzó a plantearse por qué ese orden geométrico era como era; es decir, comenzó a buscar las causas físicas cuya consecuencia fuese ese movimiento planetario tan ordenado geométricamente. Y este cambio, que dicho así parece evidente, supuso un cambio radical en la mentalidad renacentista, fuertemente impregnada todavía de la mentalidad ‘científica’ clásica.

Para Kepler, el Sol no era únicamente el ‘centro del universo’, sino que era el causante (causante físico) de que los planetas giraran alrededor de él, y que cada uno de ellos lo hiciera con su trayectoria y velocidad respectivas.

Y esta idea fue totalmente innovadora, ya que hasta la fecha no se había hecho cuestión (a fondo) de por qué se movían los planetas; o, en todo caso, se pensaba que se movían bien por arrastre de las bóvedas celestes sobre las que se encontraban, o por una especie de energía interna que poseían per se, en  sentido animista o hilozoísta (Tales de Mileto). Por lo general, sus colegas se apoyaban en la física aristotélica, que entonces era consideraba definitiva. Sin embargo, él intentó fundar la explicación en una serie de causas de carácter mecánico expresables matemáticamente. Sí, los planetas fueron creados por el Creador, pero funcionan por sí mismos, y hay que buscar dichas causas. Y en esto Kepler fue un auténtico incomprendido entre las grandes figuras de la época, incluso el famoso Tycho Brahe, aunque otros le apoyaban, como su propio maestro.

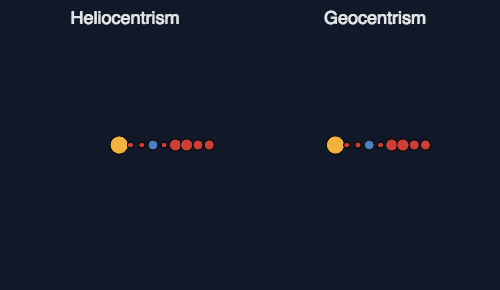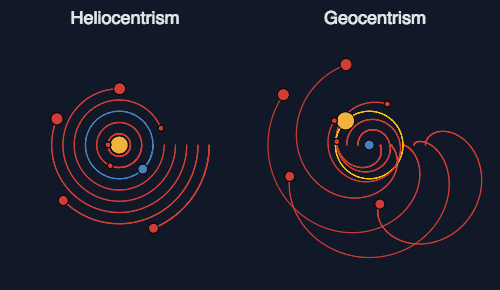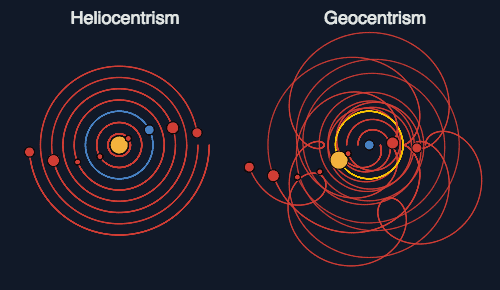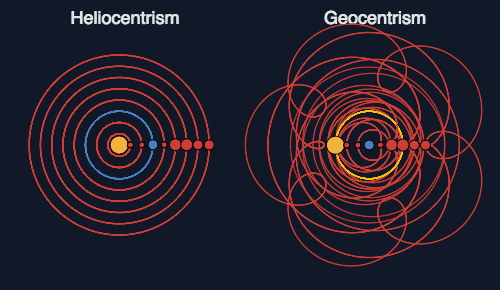
Pues bien, gracias a esta aportación kepleriana se comenzó a pensar que los movimientos de los astros ya no correspondían a una especie de dibujo geométrico realizado por la mente divina… y ya está, sino que respondían a fuerzas físicas que podían ser expresadas matemáticamente. En este sentido, el hecho de coger el modelo copernicano frente al ptolemaico (entonces imperante) simplificaba mucho el esquema, ya que era posible establecer una relación armónica (todavía por definir) entre las distancias de los planetas al Sol y sus velocidades respectivas, tal y como se puede ver gráficamente en este gif:

A mi modo de ver, más que la definición de sus leyes, la importancia de Kepler fue ésta: el cambio del paradigma clásico-renacentista al científico-moderno. Esta transición de Kepler se puede observar en sus publicaciones, tal y como nos explica F.J. Luna. Un primer esbozo fue el de asociar a los espacios interplanetarios los sólidos platónicos (tal y como se explica en el Timeo) los cuales debían encajar entre los seis planetas conocidos hasta la fecha. Estos sólidos tenían algo de mágico, o de místico: a causa de sus propiedades geométricas (convexos, caras formadas por poliedros regulares, en cada vértice se unen el mismo número de caras, simétricos respecto a un punto, eje o plano) sinónimo de perfección, se les había atribuido un elemento constitutivo de la naturaleza (fuego, tierra, aire, agua… y el mismo cosmos).

Pues bien, la intención de Kepler era mostrar cómo el Creador había ajustado los cielos a los cinco sólidos regulares, en función de cada cual el planeta ajustaría la razón de su movimiento. De hecho, llegó a publicar que esto era efectivamente así: si los desplazamientos de los planetas debían responder a leyes matemáticas, lo lógico era que se ajustaran a las matemáticas conocidas hasta la época. Y además, el hecho de que los sólidos platónicos sirvieran de base para la organización de los planetas, conllevaba un simbolismo armónico y místico evidente. Gracias a ello, la mente humana podía alcanzar a comprender (geométricamente) la obra divina del cosmos. Para Kepler existía una similitud entre la razón divina y la humana, capaz de comprender a aquélla. «Uno puede circunscribir un sólido platónico diferente alrededor de cada una de las primeras cinco esferas, e inscribirlo dentro de la siguiente. ¡Por tanto los cinco sólidos platónicos pueden mediar entre seis esferas!», explica Wilczek. ¿Y por qué seis? Pues porque seis eran los planetas conocidos: Mercurio, Venus, la Tierra, Marte, Júpiter y Saturno. De esta manera, inicialmente pensaba que podía conocer las distancias relativas entre los distintos planetas y el Sol. Estaba convencido de que había hallado el plan de Dios. Así lo expresa él en su Mysterium cosmographicum: «me siento transportado y poseído por una euforia inenarrable ante el espectáculo divino de la armonía celestial».

Sin embargo, aunque Kepler asumió esta disposición geométrica del cielo, no asumió la explicación de fondo ya que, si bien la arquitectura era esa, lo que había que hacer —como sabemos— era ir más allá de la explicación teológica o animista, para acudir a una explicación en términos empíricos, observables y medibles, de alguna manera experimentables. Sí, Dios construyó así los cielos, pero el funcionamiento de estos se debía a causas intrínsecas al mismo sistema celeste. El asunto era concretar esas causas y los movimientos a que daba lugar.

Porque concretar esas leyes según las cuales los planetas giraban alrededor del Sol no fue una tarea nada sencilla, por otra parte. Que entre la distancia y la velocidad había algún tipo de relación, era algo evidente; la cuestión era averiguar cuál. Para ello estableció algunas variables, como las distancias y las velocidades planetarias, o distintos ámbitos celestes (el propio del Sol, el de los cuerpos fijos y el de los cuerpo movientes) y comenzó a investigar. Probó con todo tipo de series geométricas, aritméticas… funciones trigonométricas… pero ninguna le acababa de dar resultado. No sabía hacia dónde ir; su única vía era ir probando ‘por tanteo’. Pero no cejaba en el empeño, pues si el orden del cosmos era divino, consecuentemente era también matemático, y por tanto debía ser posible averiguar ese principio matemático válido para todos los casos.

Con el tiempo, fue abandonando su idea de mantener viva la hipótesis de que los planetas se movían siguiendo las trayectorias marcadas por los sólidos platónicos, para establecer al Sol, no únicamente como centro del sistema solar, sino como causante físico directo del movimiento de estos (idea ajena al pensamiento de Copérnico). Él pensaba que, o bien las ‘almas de los planetas’ se debilitaban conforme más lejanos estaban del Sol, o bien sólo éste estaba animado, y su influencia en los planetas se debilitaba con la distancia, asumiendo que sólo había una única fuerza en el sistema solar y que dependía del astro rey. Y, paralelamente, siguió dos líneas de trabajo colaterales: mejorar en la fiabilidad de los datos observados (motivo por el cual acudió a Tycho Brahe, el cual disponía de muchos más medios), así como profundizar en sus conocimientos matemáticos.

Vio con claridad la relación que hay entre el tiempo de revolución y el incremento de los radios de las órbitas. Pero esta relación no era una relación directa, sino que debía intervenir otra variable, o debía ser de otro modo. comenzó a considerar potencias de las distintas variables para establecer las razones matemáticas, probando para que los resultados matemáticos se ajusten a los datos observados. Su procedimiento fue un auténtico proceso por tanteo, algo de lo que el propio Kepler era consciente. Su profesionalidad y su inquietud le llevó a profundizar en las matemáticas (así como en el significado físico de las modificaciones de las variables), explorando cada vez más los límites de la ciencia de su tiempo. Una ciencia dependiente en gran medida de la cosmovisión científica clásica y de la comprensión teológica del mundo, en la que no cabía (¡era algo impensable en el espíritu de la época!) la búsqueda de las causas físicas. Para Kepler, sin embargo, no eran problemas distintos, sino distintas dimensiones (geométrica, teológica, física) de un mismo problema. Con el tiempo, iría averiguando sus famosas leyes, pero eso ya es otra historia.

Ya en breve, con Galileo y sobre todo con Newton, el paradigma cambió definitivamente. El mundo ya no era considerado como ‘la obra de Dios’, comenzando a ser considerada independiente, no sólo de Dios, sino también del hombre. Surgió en el imaginario de los científicos de la época la posibilidad de una descripción o explicación objetiva de la Naturaleza atendiendo a sus propios procesos; Naturaleza que ya no era más que un acontecer de procesos regulares en el espacio y en el tiempo, susceptibles de ser expresados matemáticamente. Esta tendencia se extendió durante las siguientes generaciones, en las cuales la mecánica newtoniana se fue aplicando a dominios cada vez más amplios de la Naturaleza: ya no sólo el gran desarrollo de la mecánica durante el siglo XVIII, sino también el de la óptica y la termodinámica durante las primeras décadas del XIX. Y en breve, y gracias al desarrollo de la técnica, a esos otros ámbitos recónditos sin la cual no hubiéramos podido tener noticia de ellos (astronomía, química, electricidad).